
Prime1 = randprime ( 3, 2 **key_size / 2 ) Return lastremainder, lastx * ( - 1 if aa 2 **key_size : Lastremainder, (quotient, remainder ) = remainder, divmod (lastremainder, remainder ) X, lastx, y, lasty = 0, 1, 1, 0 while remainder : Lastremainder, remainder = abs (aa ), abs (bb ) #The following two functions will return a value of d when you pass it the parameters public-key exponent and totient. #Importing the greatest common divisor method from math from math import gcd #Importing the SymPy library from sympy import randprime
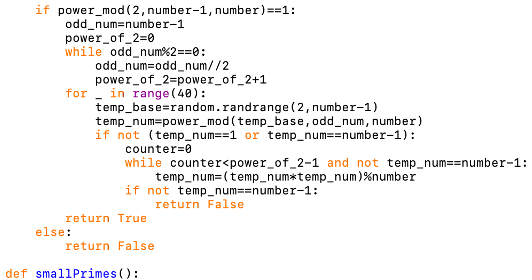
Our code should have the logic to ensure that the RSA modulus r is less than 2^KeySize. Therefore, we need to check in our code that the RSA modulus r is not too large for the desired key size. For example, if we want to use a 8-bit key, the RSA modulus r cannot exceed 2^8 = 256. IMPORTANT NOTE: - Talking about the key size (in bits), it is the RSA modulus r that is constrained. And, as we know, the RSA modulus r is used later on in the encryption and decryption processes. r = p* q (remember that the fundamental basis of the RSA Asymmetric Encryption Process is the fact that it is extremely easy to compute the RSA modulus r = p*q, but very difficult to reverse). Once we have the two (different) prime numbers, we should calculate the RSA modulus r. We need to ensure that the two prime numbers generated are different. SymPy has a method called randprime() that can generate a random prime between two numbers. We are going to use the SymPy built-in Python module. The very first step is to generate two prime numbers, p and q.

Implementing the RSA Asymmetric Encryption Process in Python The code has been broken down into three distinct tasks - Key Generation, Encryption and Decryption.

This technical article walks the reader through the Python code that can be used to implement the RSA Asymmetric Encryption Process.


 0 kommentar(er)
0 kommentar(er)
